Глава 4 Как геометрия делает красивое прекрасным

Глава 4

Как геометрия делает красивое прекрасным

Нельзя сказать, что использование геометрии само по себе делает вещи красивее. Но в названии этой главы мы хотим подчеркнуть, что во всех культурах высоко ценились качественно сделанные вещи, а качество во многих случаях достигалось именно благодаря математической точности. Именно в этом смысле Эрнст Гомбрих говорит о роли геометрии в искусстве в своей книге «Чувство порядка», посвященной декоративно-прикладному творчеству.

Действуйте геометрически

Аэропорты всего мира за несколько лет превратились в настоящие торговые центры. В них можно найти буквально все: киоски, аптеки, бары, рестораны, магазины часов, одежды, подарков и электроники. Пассажирам, ожидающим вылета, доступны самые разные товары.

Но магазинами дело не ограничивается: в некоторых аэропортах, в частности в сингапурском аэропорте Чанги, пассажиры могут посетить бесплатные выставки.

В одном из вестибюлей аэропорта были установлены панели экспозиции под названием «Go Geometric» («Действуйте геометрически»). В выставке подчеркивалась связь культуры и геометрии. Кроме того, посетителям предлагалось самим создать или воссоздать геометрические узоры, которые можно встретить в образцах архитектуры и декоративно-прикладного искусства народов Азии.

Выставка «Go Geometric» в сингапурском аэропорту Чанги.

На одном из стендов можно было напечатать на бумаге марку с особым узором — бесконечным узлом, одним из символов Будды. Этот узел так назван, потому что представляет собой линию, которую можно провести, не отрывая карандаша от бумаги. Обычно он используется в украшении самых разных предметов — так, его упрощенная версия украшает тарелку, изображенную на иллюстрации.

Стенд выставки в аэропорту Чанги и описи бесконечного узла на бумаге.

Почему этот узел называется бесконечным? Очевидно, потому, что он представляет собой циклическую линию. Если мы пройдем вдоль нее, начиная из любого места, то в конце концов вернемся в начальную точку. Эта линия непрерывная и замкнутая. Форма узла определяется сеткой, на которой он изображен, и расположением самой линии узла относительно сетки.

Две фигуры называются топологически эквивалентными, если одну из них можно получить из другой путем непрерывной деформации (без разрезов), и число отверстий в фигуре при этом не меняется. Так, топологически эквивалентны кольцо и рама картины. Аналогично, топологически эквивалентными являются бесконечный узел, изображенный выше, и следующая фигура. Кроме того, обе эти фигуры обладают осевой симметрией второго порядка (относительно поворота на 180°).

* * *

ТОПОЛОГИЯ

Топология — раздел математики, изучающий формы, но не размеры, то есть не длины, углы, площади или объемы. С точки зрения топологии все объекты мягкие и деформируемые. Если путем непрерывной деформации, то есть без разрезов и склеек, двум объектам можно придать одинаковую форму, такие объекты называются топологически эквивалентными. К примеру, все многоугольники топологически эквивалентны кругу. Это же можно сказать о многогранниках и сфере. Топологически эквивалентными также являются футболка и лист бумаги с четырьмя отверстиями. В топологии определяющим свойством фигуры является число ее отверстий. Кольцо топологически эквивалентно чашке, так как и кольцо, и чашка имеют одинаковое число отверстий, в отличие от стакана, в котором отверстий нет. Точно так же эквивалентными будут ложка и вилка, так как в них нет отверстий.

Цилиндр и кольцо топологически эквивалентны.

* * *

Цикл, обладающий осевой симметрией второго порядка, проходит через три вершины сетки на каждой стороне квадрата. Это же верно и в случае, когда на каждой стороне находится всего одна вершина.

Если число вершин сетки на каждой стороне квадрата четное, имеем другую разновидность цикла, с осевой симметрией четвертого порядка (относительно поворота на 90°).

За исключением случая, когда на каждой стороне располагается всего одна вершина, различные циклы такого типа (обладающие осевой симметрией четвертого порядка) можно определить для любого числа вершин на стороне квадрата, как четного, так и нечетного. Для сетки размером 4 x 4 это будут две вершины, для сетки размером 7 x 7 — три.

Если число вершин сетки на каждой стороне квадрата четное (сетка состоит из нечетного числа клеток), то не существует цикла, проходящего через все вершины и подобного исходному узлу.

Чтобы получить бесконечный узел, проходящий через все вершины сетки, нужно, чтобы число вершин на каждой стороне квадрата было нечетным, или, что аналогично, число клеток сетки — четным.

Теорема 1: Если сетка состоит из четного числа клеток, полученный узел будет бесконечным, подобно исходному, и будет обладать осевой симметрией второго порядка (относительно поворота на 180°).

Теорема 2: Для любого числа клеток сетки n²  при n = 2·k или n = 2·k + 1 определимы k циклов с осевой симметрией четвертого порядка.

Ранее мы показали, что в сетке из 49 клеток (

n = 7 = 2·3 + 1) можно определить три цикла, обладающих осевой симметрией четвертого порядка. В сетке из 16 клеток (16 = (2·2)²) можно определить два таких цикла.

Вариации на тему симметрии

Геометрические узоры встречаются повсеместно и практически у всех народов. Первые геометрические петроглифы появились еще в древнейшие времена — их примеры найдены в пещере Бломбос (ЮАР) или в Раскрашенной пещере на Канарских островах (Испания). Узоры, созданные еще до нашей эры в Древнем Египте, Древней Греции и Византии, имеют более формальный характер. Уже в нашу эру римляне использовали геометрические узоры в мозаиках (расцвет этого вида искусства наблюдался в Венеции до начала эпохи Возрождения). В то же время был создан чисто геометрический римско-византийский узор, обладающий самоподобием (в этом он схож с фракталами).

Римско-византийский узор (ок. 700 года).

Основу этого узора составлял квадрат, разделенный на 16 клеток. Диагонали делят каждую клетку на два равнобедренных прямоугольных треугольника. Один из них окрашивался в серый цвет, другой делился на четыре подобных ему треугольника. Один из этих маленьких треугольников окрашивался в светло-серый цвет, три оставшихся вновь делились на четыре равнобедренных прямоугольных треугольника. Далее каждый из этих трех треугольников окружался еще тремя, таким образом получалось 3·3·16 = 9·16 = 144 новых треугольника. Эти действия могли повторяться бесконечно. На каждом этапе число треугольников утраивалось.

Этот узор обладает зеркальной симметрией вида cm, определяемой параллельными осями симметрии вдоль восходящих диагоналей каждой клетки.

Но есть культура, в которой искусство рисования геометрических узоров достигло поистине невероятных высот. Арабские узоры и мозаики встречаются на территории от Марокко до Индии и от Испании до Танзании. Их удивительную симметрию можно увидеть не только в мечетях, дворцах и медресе, но и в гостиницах, аэропортах и на самолетах. Исламские узоры берут начало в арабских узорах, созданных до 1000 года нашей эры.

Арабский узор (ок. 1200 года)

Этот арабский узор, которым можно целиком замостить плоскость, образован повторением шестиугольника с осевой симметрией относительно поворота на 60°. Основу узора составляет сетка из равносторонних треугольников, сочетание которых и образует основную фигуру, или лейтмотив.

Некоторые узоры отличаются тем, что построены на треугольных, а не прямоугольных сетках, поэтому обладают осевой симметрией относительно поворота на 60° и 120°. Прямой угол в узорах также присутствует, но играет второстепенную роль. В исламской культуре геометрия узоров усложнилась с появлением двойных линий — лент, сплетающихся в виде узлов. Эти узоры двумерны, но мастера, умело играя с особенностями нашего восприятия, создают эффект трехмерности. Равносторонние треугольники сетки образуют бесконечное множество составных фигур, среди которых выделяются шести- и двенадцатиконечная звезда, как в архитектурном ансамбле Альгамбра в Гранаде.

Узор в Альгамбре времен династии Насридов (Гранада, Испания, IX век).

* * *

СИММЕТРИЯ И НЕВОЗМОЖНЫЕ МИРЫ

Мы знаем, что стороны улиц наших городов представляют собой параллельные прямые. Но мы не удивляемся, когда видим, как вдали, на горизонте, эти прямые сходятся в одной точке. Из-за особенностей нашего зрения далекие предметы кажутся нам меньше. Сочетание симметрии и технологий может порождать новые миры — невозможные, но отчасти реалистичные. Достаточно взять любую фотографию, отразить ее половину по вертикали или горизонтали и приложить к оригиналу. На двойном изображении мы увидим две параллельные улицы, симметричные друг другу.

Улица в японском городе Канадзава и симметричная ей.

* * *

К сожалению, о том, как были выполнены мозаики Альгамбры, и о том, как строились правильные девятиугольники в то время, известно очень немногое (в XVIII веке Гаусс доказал, что построить правильный девятиугольник при помощи циркуля и линейки невозможно). Остается лишь строить догадки. Впрочем, далее вы увидите, что в некоторых культурах для рисования узоров до сих пор используют те же методы, что и в далеком прошлом.

Индийские орнаменты колам

Каждое утро женщины с юга Индии, особенно из штатов Тамилнад и Керала, проводят у дверей своих домов ритуал: они рисуют на земле рисовой мукой или мелом ряд геометрических фигур, которые затем могут раскрашивать в яркие цвета. Эти фигуры — колам — отличаются большим разнообразием и могут иметь вид как маленьких и простых изображений цветов, так и сложнейших геометрических узоров.

Колам — это не просто искусство. Линии и фигуры в нем обычно строятся на сетке точек, заранее размеченных на земле. Кроме того, колам состоят из меньших фигур, как правило, симметричных и повторяющихся по заданной схеме, которая также определяется формой исходной сетки из точек. На фотографии изображен колам с двумя перпендикулярными осями симметрии, начерченный на основе восьмиугольной сетки из точек.

Женщины рисуют колам в городе Ченнаи, штат Тамилнад (Индия).

Как правило, узоры колам рисуют женщины, вместе с другими работами по дому. Но иногда к ним присоединяются и мужчины — просто для эстетического удовольствия.

Только в одном случае колам должен рисовать мужчина — во время особого ритуала, посвященного богине-матери Бхагавати в штате Керала. Этот ритуал называется Бхагавати севаи, и проводить его может только жрец-мужчина, который и должен нарисовать особый колам — падман (лотос).

Существует два основных вида узоров колам. К первому относятся узоры, подобные изображенному на предыдущей странице. Они состоят из двумерных фигур, заполняющих сетку из точек. Узоры второго типа состоят из одной или нескольких непрерывных линий, которые проходят через все точки сетки и образуют одну или несколько фигур.

Все колам начинаются с построения на земле сетки из точек, расположение которых зависит от свободного места. Колам могут заранее изображаться на бумаге, особенно если речь идет об очень сложных узорах или фигурах больших размеров. Проводить линии, соединяющие точки, нужно без ошибок — исправления не допускаются. Узоры колам не имеют особых названий и обозначаются по принципу подобия — «звезда», «лотос», «кокосовая пальма», «повозка» и так далее. Линии, соединяющие точки, имеют форму восьмерок, или знака бесконечности.

Колам, составленный из элементов меньшего размера, изображенных одной линией.

Сходство со знаком бесконечности не случайно — в этом регионе непрерывные линии подобной формы обозначают бесконечный цикл жизни: рождение, расцвет, увядание.

Тщательно изучив боковые кривые на изображенном выше коламе, мы увидим, в каких случаях их можно изобразить одной линией. Четыре боковые фигуры представляют собой прямоугольники и изображены на сетках точек размерами 2 x 7. Все точки соединены одной линией. Аналогично можно соединить точки в сетках размерами 2 х 3 и 2 х 5.

Но провести такую линию на сетке 2 х 4 не удастся. В этом случае потребуются две линии, симметричные по вертикали и горизонтали.

Можно ли соединить все точки сетки одной линией, зависит от того, сколько столбцов в сетке — четное это или нечетное число. Пронумеруем столбцы слева направо и увидим, что кривая на сетках размером 2 х З, 2 х 5 и 2 х 7 проходит через столбцы под номерами: {1, 2, 3}, {1, 2, 4, 3} и {1, 2, 4, 6, 7}. Для четного числа столбцов подобное невозможно.

Чтобы построить непрерывную линию, проходящую через все точки сетки двух строк А и В и N столбцов (где N нечетное, то есть имеет вид N = 2·k + 1), нужно следовать алгоритму:

N = 2·k + 1:

к четное: {А(1), В(2), А(4), В(6), …, А(2·k), В(N)};

к нечетное: {А(1), В(2), А(4), В(6), …, А(2·k), A(N)}.

Некоторые колам образованы одной кривой, подобно бесконечному узлу, но большинство узоров состоят из нескольких линий.

Колам из трех линий.

Этот колам образован тремя кривыми. Две из них одинаковы: одна получается из другой поворотом на 90°. Обе эти кривые симметричны относительно поворота на 180°. Третья кривая образует фигуру, симметричную относительно поворота на 90°. Она построена на двойной сетке из 25 точек, которые расположены в виде двух квадратов размерами 3 х 3 и 4 х 4, причем первый находится внутри второго.

Колам.

Традиция изображать колам на юге Индии насчитывает несколько веков, и ее истоки, возможно, лежат в культурах Центральной Африки. В этих узорах математическая мысль состоит не столько в симметричности итоговых фигур, сколько в четких методах построения. Именно женщины являются хранителями многовековой традиции и математических знаний, которые ежедневно используются в домашнем хозяйстве. Методы изображения колам передаются от матери к дочери, совершенствуются и достигают таких высот, что ими восхищаются математики всего мира.

Лозоплетение

В одиннадцатой главе трактата «Дао дэ цзин» отмечается, что полезность колес, сосудов и окон проистекает из их пустоты. В самом деле, люди с доисторических времен стремятся отделить небольшие участки бесконечного пространства, которое нас окружает, создавая границы: для колеса нужна окружность, для сосуда — сферическая поверхность, для окна — плоская стена с отверстием в нем.

В разные годы были созданы самые разные плоские и криволинейные поверхности из бесконечного множества материалов и бесконечным множеством способов. Чаще всего для создания поверхностей и объемных тел применялось плетение волокон растений — этим методом создаются как плоские поверхности — циновки рогожи, стены и крыши домов, так и объемные фигуры — корзины, клетки, загоны для птицы и мячи для игры в сепактакрау (разновидность волейбола в Юго-Восточной Азии, но игра происходит не руками, а ногами).

Творческие способности и умения мастеров со всего света заслуживают восхищения как с художественной точки зрения, так и с точки зрения технологий. Паулус Жердес, исследователь этноматематики из Мозамбика, изучил узоры и формы, применяемые мастерами плетения из лозы. Среди геометрических задач, связанных с лозоплетением, выделяется следующая: каким должен быть угол сгиба, если нужно обернуть один прут вокруг другого прута такой же толщины? Ответ — 60° — определяется при помощи тригонометрических расчетов. На практике этот угол определяется складыванием лозы вдвое, как показано на рисунке.

Богатство орнаментов в лозоплетении.

Мячи для игры в сепактакрау

Мячи для игры в сепактакрау во всей Юго-Восточной Азии изготавливаются из ротанга, который также используется для изготовления мебели. Ротанг напоминает ивовый прут, но в сечении эти стебли ротанговой пальмы не округлые, а плоские. Ротанг гибкий, но очень прочный, и сломать его нелегко даже при ударах ногами, как во время игры в сепактакрау.

Мастер демонстрирует мяч для игры в сепактакрау.

Мастера, изготавливающие плетеные мячи, не используют никаких схем и не проводят никаких вычислений, но наблюдая за ними во время работы, сложно поверить, что почти идеальную сферу можно изготовить без помощи математики.

Впрочем, математика все же используется, хоть и не в явной форме.

В математике сфера определяется как множество точек, расположенных на одинаковом расстоянии от точки, называемой центром. Однако при изготовлении мячей для игры в сепактакрау это определение бесполезно. Суть метода плетения идеальных мячей (если пренебречь неизбежными погрешностями и неровностями самого ротанга) заключается не в определении центра и радиуса сферы, а построении многогранника постоянной кривизны. Мастер начинает работу с того, что сплетает пять стеблей ротанга в форме как можно более правильного пятиугольника. Затем мастер выбирает несколько вершин пятиугольника и продевает в них новые стебли. Концы этих стеблей связывают, и получается окружность, определяющая диаметр мяча.

Постепенно по ходу плетения появляются пятиугольные грани — сначала как промежутки между прутьями, которые постепенно заполняются. По сути, полученный мяч по форме представляет собой икосаэдр с отсеченными вершинами — пирамидами с пятиугольным основанием. Разрезав эти пирамиды горизонтально пополам, получим 20 пятиугольных отверстий. Закрыв эти отверстия гранями, имеем полуправильный многогранник — усеченный икосаэдр, имеющий 60 вершин, 90 ребер и 32 грани (20 из них имеют форму шестиугольников, 12 — форму пятиугольников). Именно этот многогранник и плетет мастер. Ротанг распрямляется, и в результате мяч обретает постоянную кривизну. Пересечения трех стеблей из пучков в шесть стеблей определяют 20 шестиугольных граней мяча.

Убедитесь в этом сами.

Шары темари

Японские шары темари имеют китайское происхождение. Изначально их изготавливали из оленьих шкур для придворных, которые использовали темари для игр. Когда придворные дамы начали ткать шары из шелка, темари обрели новую роль и стали использоваться в качестве украшений. Даже проводились конкурсы на лучший шар темари с самым сложным узором и искусным сочетанием цветов.

Искусство плетения шаров темари восходит к 1000 году нашей эры и передается из поколения в поколение, от матери к дочери. Со временем темари становились все более популярными, возникали новые техники их изготовления. С появлением резиновых мячей интерес к темари надолго угас, но сегодня это традиционное искусство вновь обрело былую популярность, и в Японии даже организованы специальные общества, посвященные темари.

Японские шары темари.

В центре темари находится шар из пенопласта или мягкого пластика, куда удобно втыкать булавки. Узоры на ткани шаров преимущественно геометрические и отличаются невероятной сложностью.

При изготовлении шаров темари очень полезной оказывается раздвоенная линейка в форме буквы V с углом раствора в 72°, которая, по сути, представляет собой две линейки с соединенными концами. Этот инструмент нужен потому, что большинство узоров темари представляют собой замощения сферы, основанные на додекаэдре. Это означает, что мастерам нужно работать с правильными пятиугольниками и системой из пяти радиальных осей. Если мы разделим полный круг (360°) на пять частей, то получим угол раствора линейки — 72°.

Одна из первых задач, которую требуется решить при изготовлении темари, касается разделения поверхности шара на восемь равных частей. Для этого нужно воспользоваться основным различием между плоскостью и криволинейной поверхностью, то есть сферой. На плоскости сумма углов треугольника всегда равна 180°, а на сфере она может составлять 270°.

Поверхность темари делится на восемь частей следующим способом. Сначала на шаре булавкой отмечается произвольная точка. Затем вокруг шара оборачивается лента так, что она проходит через отмеченную точку дважды. Далее эта точка отмечается на ленте, и лента обрезается. Так определяется длина окружности шара. Теперь лента складывается пополам так, и на ней отмечается место сгиба. Затем лента сгибается еще раз, и метки ставятся на каждой из ее половин. Таким образом отметки на ленте указывают ее четверть, половину и три четверти длины.

Теперь нужно приколоть ленту к шару булавкой и обвязать ее вокруг шара. Воткнем в шар еще одну булавку посредине ленты. Эта булавка укажет «южный полюс», предыдущая — «северный полюс». Повернув шар так, чтобы лента располагалась перпендикулярно оси, проходящей через полюса, воткнем булавки туда, где находятся отметки на ленте. Таким образом, в шар будет воткнуто в общей сложности шесть булавок, которые укажут вершины шести равносторонних сферических треугольников. Однако углы этих треугольников будут равны не 60, а 90°. На поверхности сферы углы равносторонних треугольников прямые. Три перпендикулярные оси (большие круги), определяемые этими шестью булавками, делят поверхность сферы на восемь равных частей.

Эти оси могут стать основой для простого узора из цветных нитей. Отметив другие меридианы или параллели, мы разделим сферу на большее число частей, как показано на фотографии слева на стр. 115. В узоре на этом шаре выделен экватор шара, а из полюсов проведены меридианы так, что образуется 24 двуугольника (по 12 каждого цвета) в 15° каждый. Остальные два шара, изображенные на фотографии, разделены на пятиугольные грани, подобные додекаэдру.

Основой для узора на шаре темари может быть не только додекаэдр, но и любое другое платоново тело.

* * *

МУЗЫКА ГАМЕЛАНА

Гамеланы, народные оркестры островов Бали и Ява (Индонезия), состоят из одного или двух больших гонгов, двух барабанов, как минимум четырех пар тарелок, двух групп маленьких гонгов по 8-14 в каждой и флейт. Наиболее характерная секция гамелана — металлические ксилофоны разных размеров, состоящие из 7-12 брусков, на которых играют специальными молоточками.

Композиции, исполняемые гамеланами, делятся на ярко выраженные циклические секции, описываемые степенями двойки. Эти секции состоят из 2, 4, 8, 16 или 32 тактов. Степени двойки также определяют скорость исполнения: орнаментирование исполняется в 4 или 8 раз быстрее основной мелодии, а та, в свою очередь, в 4 или 8 раз быстрее, чем упрощенные версии мелодии. Удвоение скорости исполнения способствует сохранению ритма и придает музыке характерную динамичность.

* * *

Салфетки и оригами

Во всех ресторанах крупнейшего архипелага мира, Индонезии, бумажные салфетки складывают особым образом. В любом индонезийском варунге салфетки складываются своим способом, но официантки во всех ресторанах, от запада Суматры до востока Папуа, умеют складывать салфетки в характерном индонезийском стиле.

Стол в индонезийском варунге.

Схема складывания салфеток в трех разных кафе.

Квадратная салфетка складывается так, что линии сгиба делят прямой угол при одной из ее вершин на три равные части. Таким образом получается симметричный четырехугольник с прямым углом, углом в 30° и двумя углами в 120°.

Салфетка, сложенная в индонезийском стиле.

Долгое время я думал, что официанты складывают салфетки так же, как я, то есть прикладывают угол салфетки к середине противоположной стороны:

Схема складывания салфетки, в которой угол накладывается на серединный перпендикуляр так, что нижняя вершина остается на своем месте.

Получится прямоугольный треугольник. Один из его катетов равен половине гипотенузы, следовательно, угол этого треугольника равен 30°. Когда мне довелось увидеть, как официантки складывают салфетки, я решил, что мое предположение справедливо — они явно прикладывали угол салфетки к середине противоположной стороны.

Однако я ошибался. Расспросив официанток, я понял, что они в самом деле применяли геометрический метод, но далекий от моих предположений, — они старались согнуть салфетку так, чтобы разделить угол при вершине в соотношении 1:2. Вместо того чтобы прикладывать угол салфетки к середине противоположной стороны, они прикладывали сторону к центру салфетки, не складывая ее. Иными словами, они проводили биссектрису оставшейся части угла, полученного при сгибе. Этот метод был внешне неотличим от моего, и я смог понять разницу, только тщательно расспросив официанток.

Математическая идея, на которой основан этот метод, такова: 3 = 1 + 2. Обозначив через R оставшуюся часть угла, полученного при сгибе А, получим:

90° = R + 2·A.

Так как мы хотим, чтобы согнутый угол совпадал с оставшимся углом, прямой угол салфетки окажется разделен на три части:

Проекция математических идей заключается в том, чтобы при помощи математики объяснить события, которые необязательно имеют математическую природу либо действительно описываются математически, но не так, как кажется. Не стоит пытаться математически объяснить мысли и действия других людей, иначе легко попасть в неловкое положение: человек, который нам покажется несведущим в математике, может оказаться гораздо более компетентным, чем многие вокруг.

Поделитесь на страничке

Следующая глава >

Геометрические рисунки для срисовки (23 фото) 🔥 Прикольные картинки и юмор

Далее предлагаем геометрически рисунки для срисовки.

Рисунок для срисовки медведь.

Картинка голова оленя.

Геометрические фигуры.

Геометрический рисунок для срисовки.

Геометрический рисунок олень.

Геометрический рисунок голова льва.

Рисунок голова единорога.

Рисунок бриллиант.

Картинка для срисовки фламинго.

Картинка голова собаки.

Рисунок для срисовки сова.

Геометрический рисунок для срисовки.

Картинка геометрические фигуры.

Геометрический рисунок лиса.

Геометрическая картинка олень.

Геометрический рисунок для срисовки.

Рисунок снежинки.

Геометрический рисунок голова собаки.

Геометрический рисунок для срисовки.

Рисунок медведь.

Рисунок голова волка.

Геометрическая картинка для срисовки.

Рисунок лисенок.

Мне нравится8Не нравится1

Будь человеком, проголосуй за пост!

Загрузка…

---

 

Красивые картинки название геометрических фигур (35 фото)

Если у вас есть ребенок дошкольного возраста и вы хотите ,чтобы он хорошо знал названия фигур,то данная статья как раз для вас!В ней вы найдете яркие и красивые картинки названия геометрических фигур.Все картинки находятся в свободном доступе,так что вы с легкостью можете сохранить их себе на устройство.

Цветные картинки с надписями

Различные геометрические формы на английском

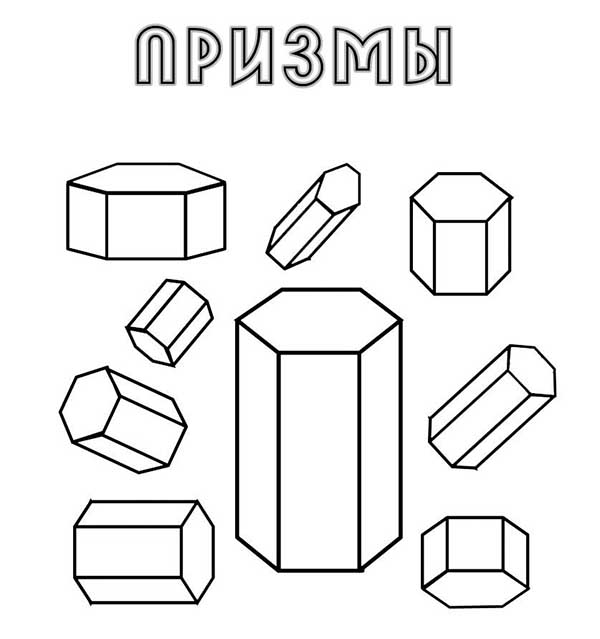
Различные виды призм

Красочные картинки выпуклых фигур

Названия объемных геометрических фигур

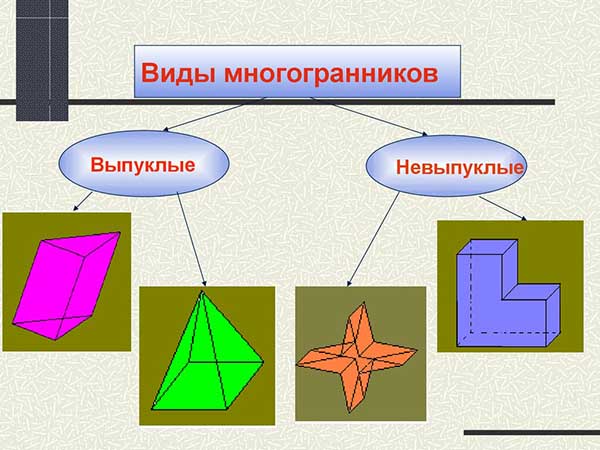
Подробная схема про виды многогранников

Виды правильных многогранников

Красивая картинка объемных фигур

Наглядное изображение пирамиды

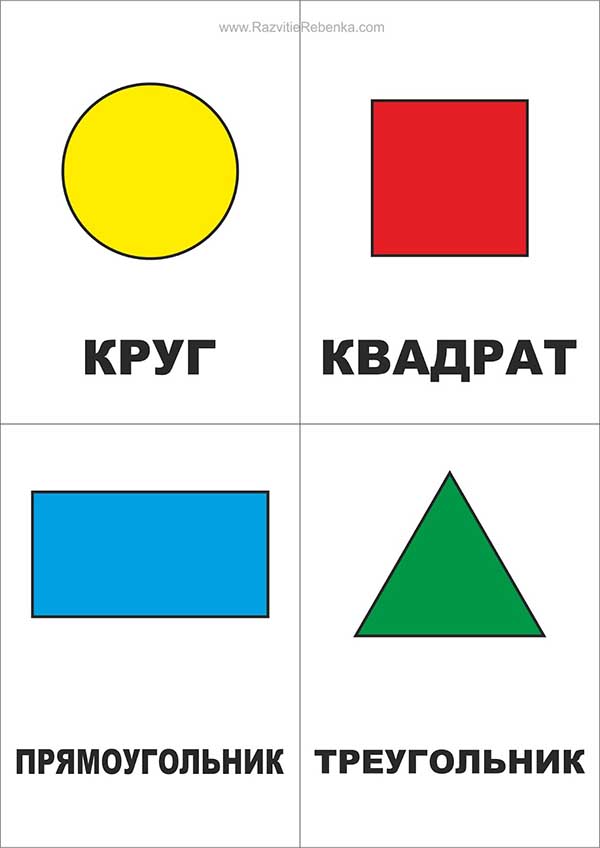
Основные названия геометрических фигур

Множество плоских и объемных фигур

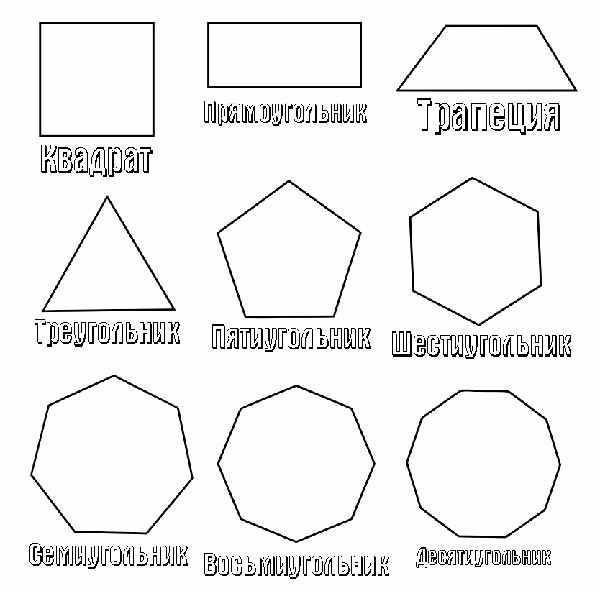
Понятная картинка о названии геометрических фигур

Красочная картинка про виды многогранников

Ромб фиолетового цвета

 

Яркие картинки фигур для детей

Усеченный конус оранжевого цвета

Обычный конус серого цвета

Один из видов выпуклых фигур- октаэдр

Наглядное изображение прямоугольника

Пятиугольник в фиолетовом цвете

Равнобедренный треугольник голубого оттенка

Картинка квадрата для детей

Параллелограмм в зеленом цвете

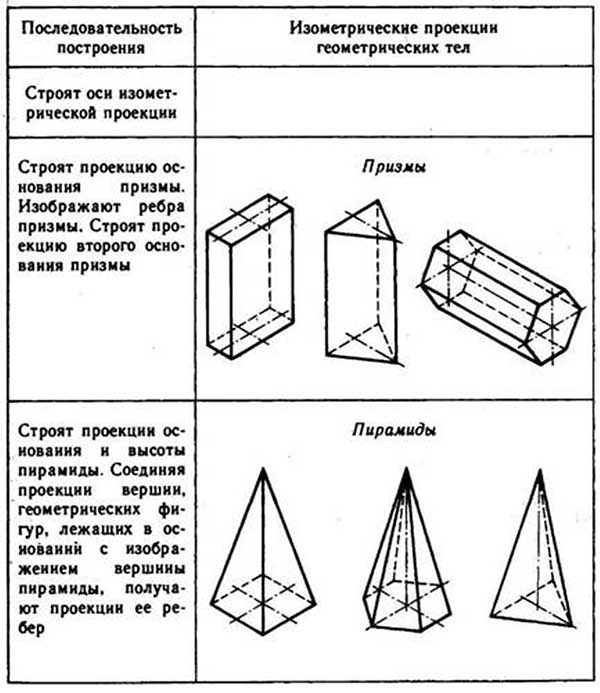
Названия и способ построения выпуклых фигур

Названия разнообразных геометрических форм

Идеальный овал розового цвета

 

Красивая картинка полукруга в оранжевом цвете

 

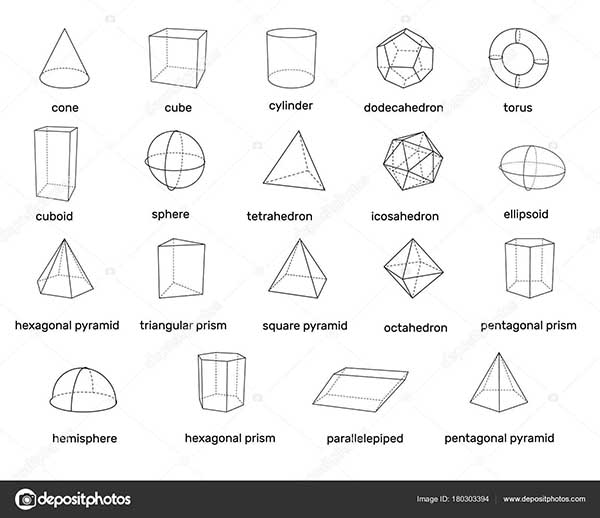
Красочные картинки геометрических фигур с названием на английском

Яркая и понятная картинка о геометрических формах

Конус обыкновенный в голубом цвете

Яркие картинки геометрических фигур с названием

Красиво изображенный куб голубого цвета

Круги в реальной жизни

Интересная интерпретация названия геометрических фигур

Photostocky – это бесплатный сервис картинок, открыток и Gif-анимации, где вы сможете найти любой медиа-контент по вкусу. Мы собрали только лучшие, красивые и прикольные картинки со всей сети Интернет, которые находятся в свободном доступе и вы с легкостью сможете скачать их бесплатно.

Вы можете помочь проекту и поделиться картинками в соц. сетях Facebook, VK (Вконтакте), Одноклассниках или отправить в мессенджерах Viber, Telegram, WhatsApp, Skype.

Вы также можете использовать картинки для вебсайтов и помочь нашему проекту оставив обратную ссылку на источник, мы вам будем очень признательны, ведь наши редакторы стараются для того, чтобы собрать для вас только лучший контент из сети.

 

 

Если Вам понравилась статья, Вы можете поделиться ею в социальных сетях или поставить оценку данной статье

Картинки названия геометрических фигур для детей

Удивительный мир геометрических фигур! Давайте начнем изучать основы геометрии с этих чудесных картинок для детей с названиями. Уже в три года названия геометрических фигур постепенно вводят в активный словарь детей. Фигуры бывают разные: плоскостные и объемные. Фигуры простейшие изучают в математике в начальной школе: они могут состоять из отрезков и замкнутых линий. А планиметрию и стереометрию проходят в более старших классах. Желаем, чтобы знакомство с геометрическими фигурами приносило детям радость. Ну, что ж, приступим…

 

Этот удивительный мир геометрических фигур!

 

Плоскостные геометрические фигуры

 

Объемные геометрические фигуры

 

Из таких фигур можно строить замки!

 

Простейшие (основные) геометрические фигуры

 

Геометрические фигуры на плоскости

 

Какие геометрические фигуры изучают планиметрия и стереометрия

 

Виды фигур на плоскости

 

Криволинейные треугольники

 

Круг Овал Квадрат Прямоугольник

 

Овал и эллипс похожи, но различия есть

 

Трапеция Ромб Четырехугольник Параллелограмм

 

 

Правильные многоугольники

 

Треугольник Различные виды треугольников

 

 

Куб

 

 

Шар

 

Цилиндр

 

Конус

 

Пирамида

 

Параллелепипед

 

Призма

 

Различные виды призм

 

Усеченный конус

 

 

Усеченная пирамида

 

Правильные многогранники

 

Октаэдр

 

Икосаэдр

 

 

Додекаэдр

Картинки названия геометрических фигур (30 фото) • Прикольные картинки и позитив

Геометрические фигуры нужно знать для лучшего понимания предмета. Смотрите далее красивые картинки про названия геометрических фигур.
Прямоугольник, ромб, круг.
Параллелепипед, шар, конус.
Круг, квадрат, овал.
Сложные геометрические фигуры с названием.
Ломанная, многоугольник, отрезок.
Конус, цилиндр, сфера.
Картинка про название геометрических фигур.
Полукруг, треугольник, трапеция.
Квадраты, круги, овалы.
Разные фигуры из геометрии.
Параллелограмм, восьмиугольник.
Квадрат, шестиугольник, семиугольник.
Звезда, призма, сфера.
Предметная картинка про геометрические фигуры.
Большой красный конус.
Оранжевый ромб.
Синий куб.
Название геометрических фигур
Геометрические тела.
Разные пирамиды.
Простая картинка названия геометрических фигур.
Фиолетовый ромб.
Красивый конус.
Овал, трапеция, ромб.
Много фигур из учебника геометрии.
Куб, сфера.

Сердце, звезда, овал.
Геометрические фигуры и их названия.

10 стильных идей для вашей квартиры

Многие тренды в дизайне интерьера приходят и уходят, но некоторые задерживаются так надолго, что уже трудно представить индустрию без них. Использование геометрических узоров — один из таких. Причина их популярности в том, что геометрические формы универсальны. Они могут быть вписаны в любой интерьер, независимо от стиля. Круги, квадраты, зигзаги, прямоугольники, шестиугольники занимают одну из главных позиций в мире дизайна. ReRooms собрал десять стильных идей использования геометрических узоров. 

Мы советуем использовать геометрические узоры в интерьере очень внимательно и осторожно, потому что, например, шахматный рисунок неоновых цветов привнесет в помещение излишнюю динамичность и яркость. Находиться в такой комнате будет очень некомфортно. С аккуратностью нужно сочетать несколько различных фигур в одном интерьере.

В каких стилях применяются геометрические фигуры 

Дизайнеры очень любят этот элемент декора, так как он всегда добавляет необычности. Такой узор может кардинально изменить внешний вид и, как следствие, восприятие вашей комнаты. 

Геометрические узоры можно использовать в этих стилях:

Сейчас мы расскажем вам, где и как лучше всего применять этот рисунок.

1. Геометрические узоры и мебель

В мебели можно увидеть практически все геометрические фигуры, которые только существуют. Квадраты, треугольники и круги становятся идеальной формой в создании необычных и неповторимых предметов меблировки. Нет сомнений, что такая мебель станет ярким акцентом в вашей квартире. Прямоугольники, квадраты и круги — идеальная форма для создания столов и удобных кроватей.

Не стоит забывать, что выразительность мебели зависит не только от ее формы, но и от расцветки и материалов. Неоспоримый плюс геометрической мебели — универсальность.

Фото: squarespace.com

1/2

Фото: habitusliving.com

2/2

2. Геометрические узоры и аксессуары

Геометрические узоры активно используются при создании не только мебели, но и аксессуаров. С помощью необычных зеркал, ваз, цветочных горшков, часов, рамок, подсвечников и другого домашнего декора можно преобразить интерьер, не прибегая к полноценному ремонту. 

Круги, овалы, квадраты и шестиугольники активно используются для украшения текстиля, в том числе:

Все это станет интересным дополнением к однотонной мебели, присутствующей, например, в таких стилях, как минимализм или скандинавский.

Фото: squarespace.com

1/2

Фото: squarespace.com

2/2

3. Геометрические узоры и освещение

Один из самых популярных элементов дизайна интерьера — светильник с абажуром в форме алмаза. Его можно повесить возле необычного зеркала, которое состоит из маленьких кусочков, преломляющих свет. Таким образом блики заполнят все помещение и создадут атмосферу волшебства.

Светильники и лампы геометрических форм отличают строгость и лаконичность, а также простота линий и форм.

Материалы, из которых выполняются геометрические плафоны, довольно разнообразны, к ним относятся:

• металл, 

• пластик, 

• дерево, 

• стекло, 

• бумага. 

Осветительным приборам дарят формы практически всех геометрических фигур (цилиндр, конус или пирамида). Это могут быть открытые «кристаллы», выполненные из металлических стержней, или закрытые конструкции. Такой элемент декора сможет пусть и не полностью преобразить интерьер помещения, но стать его яркой и неотъемлемой частью — точно.

Фото: squarespace.com

2/2

4. Геометрические узоры на полу, потолке и стенах

Геометрических узоров можно добиться с помощью:

• обоев,

• плитки,

• деревянных элементов,

• нарисованных элементов.

Лучше всего оформлять одну из стен с помощью геометрии, чтобы не перегрузить интерьер. Например, можно оформить стену за спинкой кровати в спальне или кухонный фартук. Другие же стены лучше оклеить однотонными обоями или окрасить в пастельный цвет.

Фото: squarespace.com

1/2

Фото: squarespace.com

2/2

5. Полосы

Полосы лучше всего помогают скрыть архитектурные недостатки помещения. 

Горизонтальные 

Такие полоски визуально сделают помещению просторнее и шире и «опустят» потолок. Запомните: узкие полосы дают более выраженный эффект, однако есть опасность, что от них будет сильно рябить в глазах. Поэтому, выбирая именно этот вариант, подходите очень внимательно к выбору ширины полоски.

Вертикальные 

Такие линии способны визуально поднять потолок и сделать пространство выше. Перед тем как использовать этот рисунок, измерьте длину и высоту потолка. Если один из параметров будет больше, использовать полоску нельзя, потому что помещение будет похоже на колодец.

Полоски желательно делать одинаковыми по ширине, цвету или паттерну. Используя полоски разных цветов, подбирайте оттенки так, чтобы они сочетались между собой и не рябили. Как уже упоминалось выше, не стоит забывать, что тонкая и контрастная по цвету полоска вызывает зрительный дискомфорт. Поэтому если вы все-таки предпочитаете тонкую полоску, сделайте выбор в пользу спокойных тонов. Но если вы предпочитаете яркость и контрастность, лучше выбрать более широкую полоску. Так вы уменьшите нагрузку на глаза.

Если отказываться от яркого полосатого варианта вы не хотите, используйте рисунок зонально, например выделите часть у изголовья кровати или кухонный фартук.

Фото: cole-and-son.com

1/2

Фото: squarespace.com

2/2

6. Квадраты

Квадраты, в отличие от полос, не могут визуально расширять или сужать пространство. Однако и у этой геометрической фигуры есть свои достоинства.

Квадрат — символ стабильности и порядка, поэтому с его помощью интерьер станет более уравновешенным. Квадратными могут быть рамки, столы, осветительные приборы, ковры на полу и многое другое. Эти предметы не только придадут интерьеру завершенный вид, но и наполнят помещение атмосферой покоя.

Квадрат можно использовать не только в качестве декора, но и в отделке. Любите клетчатый рисунок? Отлично! С помощью клетчатой плитки можно выложить акцентную стену в комнате или оформить фартук на кухне. Чтобы такой рисунок смотрелся гармонично, добавьте элементы текстиля с таким же рисунком: занавески, скатерть или полотенца. В гостиной же лучше использовать подушки и покрывало.

Фото: 1.bp.blogspot.com

1/2

Фото: phrustratedphan.com

2/2

7. Зигзаг (шеврон)

Зигзаг — один из самых динамичных и ярких принтов из представленных. Одновременно в этом рисунке чувствуется игривость, большое количество энергии и непринужденность, гармоничность. Однако такого эффекта возможно добиться только в том случае, если правильно подобрать цветовую гамму и использовать его в меру. Шеврон, как правило, используют в качестве рисунка на текстиле (особенно классно он будет смотреться на ковре или постельном белье) и элементах декора. Зигзаг оживит любое пространство, где бы он ни появился, и для этого есть много вариаций его использования. Например, оформите кухонный фартук с помощью плитки с зигзагообразным рисунком.

Как мы уже упомянули, к цвету этого рисунка нужно подходить осторожно. Вы можете сделать насыщенное и яркое оформление, но только в том случае, если другие стены и декор будут приглушенных и пастельных оттенков. Только так у вас получится сбалансировать общий вид комнаты.

Фото: blogdecora.com.br

2/2

8. Круги и овалы

Они привнесут в ваш интерьер гармонию и мягкость, сбалансируют помещение, в котором находится много предметов с острыми углами. Эти фигуры можно использовать не только в качестве настенных рисунков, но и как аксессуары, в мебели и отделке текстиля.

Закругленные предметы меблировки — кровати, диваны, комоды или стулья — придадут помещению спокойствия. Тем более они подойдут к любому помещению любого стиля.
Выбирая тот или иной рисунок, главное — не перестараться. Не нужно использовать круг во всех деталях интерьера, иначе вы рискуете перенасытить помещение, в котором из-за этого будет некомфортно находиться. 

Если вы выбрали круглый ковер, на него лучше поставить квадратный столик. Такой прием касается не только кругов, но и других геометрических фигур. С помощью одной фигуры вы уравновесите другую.

Если вам хочется чего-то позитивного и легкого, тогда принт «горошек» подойдет как нельзя лучше. Его можно использовать не только в детской комнате, но и в других помещениях, например в гостиной. Главное здесь — правильно подобрать цвет и размер.
Не обязательно использовать этот принт на всей стене. Можно выделить какую-нибудь одну зону и покрыть «горошком» только часть стены. Чтобы он казался более гармоничным, продолжите рисунок на потолке, закончив композицию интересным светильником, но уже другой геометрической формы.

9. Прямоугольники

Прямоугольники, как и квадраты, выглядят в интерьере одновременно элегантно и просто, не привлекая к себе много внимания. Они отлично сочетаются с круглыми и овальными формами, квадратами. Что касается цветового решения, многое зависит не только от ваших вкусовых предпочтений, но и от метража комнаты.

Яркие цвета используйте в помещениях с большой площадью — так вы избежите перегрузки интерьера. Но в любом случае стоит дополнить кричащие оттенки нейтральными тонами. Излишняя пестрота в маленьком помещении очень быстро утомит и может вызвать головную боль. Пастельные спокойные тона используйте в маленьких комнатах — визуально помещение станет просторнее.

Прямоугольные фигуры чаще всего встречаются в отделочных материалах напольного покрытия (ламинат, паркетная доска) и в предметах меблировки. Они создают базу интерьера по отношению к другим геометрическим фигурам.

В комнате с низким потолком используйте прямоугольные формы на полу: ковер или плитку. Благодаря такой хитрости визуально он приподнимется.

Если в вашей комнате низкий потолок, сделайте акценты на полу с помощью прямоугольного ковра или плитки — зрительно он приподнимется.

Фото: dwigallery.com

1/2

Фото: trendland.com

2/2

10. Шестиугольники (соты)

Использование этой геометрической фигуры создаст впечатление, будто вашу комнату разрисовал экспрессионист-кубист. Для того чтобы ваш интерьер смотрелся оригинально, выбирайте шестиугольные тумбы, пуфы, столы для гостиной. Чтобы украсить помещение, не обязательно выбирать только мебель такой геометрической формы. Вам опять же придут на помощь элементы декора. Например, отлично украсят и освежат помещение зеркала, которые напоминают кристаллы. Тем более такой прием поможет зрительно увеличить пространство. 

Еще один способ украшения шестиугольниками — использовать их в отделке (настенная или напольная плитка). Сегодня производители предлагают много видов плитки, в том числе готовые наборы, где представлена однотонная плитка и плитка с рисунками. Такой отделочный материал можно использовать в любой комнате, например в ванной, чтобы подчеркнуть зону ванны или умывальника, или на кухне — для оформления рабочего фартука.

Фото: i.etsystatic.com

1/2

Фото: ragnoworld.com

2/2

20 красивых сайтов с не стандартной и необычной геометрией

Здравствуйте, дорогие читатели блога. В этот чудесный день я спешу представить Вам замечательную подборку красивых сайтов, в которых используется не стандартная техника геометрии. 

Что имеется в веду? Вы наверное уже привыкли к таким сайтам на которых всё стандартно. 🙂 А именно Обычные ровные блоки, в которых находится какая либо информация. А в этом случае всё наоборот, используются более кривые линии чем обычно. И согласитесь смотрится довольно красиво.

Но я бы посоветовал не слишком экспериментировать, если переборщить, то на таком сайте можно просто напросто потеряться 🙂

Так что давайте посмотрим, как это делают профессионалы.

Так же я думаю, что Вам будет интересно следующее:

webspecies.co.uk

Огромное спасибо speckyboy.com

20 035 фотографий с красивой геометрией — бесплатные и лицензионные фотографии из Dreamstime

Красивая геометрия освещенного ночного мостика. Красивая геометрия линий и форм ночного освещенного моста через реку

Черно-белая лестница, красивая геометрия, интерьер, архитектура. В Финляндии

Красивый дельфин плавает в стильном бассейне в голубой воде, геометрия спокойствие, умиротворение.

Красивая геометрия здания в Германии.

Красивая черная девушка смотрит сквозь геометрическое отверстие в бумаге. Красивая афро-американская девушка с естественным макияжем смотрит сквозь геометрическое отверстие в бумаге, пустой

Крупный план на красивой архитектурной форме геометрии. Крупным планом на красивой архитектурной геометрии формы фона современных зданий в центре Бангкока, Таиланд

Красивая геометрия лавандового поля.Валенсоль, Прованс

Красивая геометрия с синим y. Красивая геометрия

Красивая геометрия на природе, красивое ущелье. Очень красивое место в горах между небом, камнями и зеленой травой

Красивые металлические серьги сакральной геометрии. На фоне оболочки

Красивые латунные серьги с сакральной геометрией.На фоне оболочки

Красивые латунные серьги с сакральной геометрией. На фоне оболочки

.

Геометрия — красивое изображение. Изображение красивых уравнений

Мы жертвуем 10% дополнительных гонораров нашим вкладчикам в качестве стимула для борьбы с COVID-19

Похожие изображения

Красивая геометрия освещенного ночного моста

Свадебная пара в эффектный холостой день, прогулки, геометрия. Короткое свадебное платье в деревенском стиле. Девушка брюнетка. красивая невеста

Блокирует старую текстуру геометрии, цементный пол каменного кирпича красивый фон.

Блокирует старую текстуру геометрии, каменный кирпич, пол, цемент, красивый фон

Витраж в форме круга в церкви Португалии, Порту

Черно-белая лестница, красивая геометрия, интерьер, архитектура

Красивый дельфин плавает в стильном бассейне в голубой воде, геометрия спокойствие, умиротворение

Красивая геометрия здания в Германии.

Красивая черная девушка смотрит сквозь геометрическое отверстие в бумаге

Красивая геометрия лавандового поля

Красивая геометрия с синим y

Красивая геометрия на природе, красивое ущелье.

Металлические серьги с красивой сакральной геометрией

Красивый креативный медный цвет, геометрия, текстура, узор, стена, современное здание, украшение для дома и гостиной

.

Beautiful Geometry от Эли Маора

В целом, сотрудничество между искусством и наукой вызывает у меня легкую тошноту. С научной точки зрения, это похоже на щенячье отчаяние быть любимым и нормальным. «Послушайте, я не совсем ботаник, — кажется, они говорят, — я не всегда говорю непонятно на техническом жаргоне. Я умею заниматься искусством ». Между тем, кажется, что искусство имеет слишком много общего с теми разносчиками ву, которые вкладывают в свой змеиный жир (как они думают) научную гравитацию, используя термины квантовой физики, чтобы приукрасить свою чушь.

Итак, если честно, я подошел к этой совместной работе математика и художника размером с журнальную книжку со всем энтузиазмом человека, который едет к дантисту. Так получилось, что моя оценка была немного резкой, потому что искусству не позволялось доминировать, как это обычно бывает. Здесь мы получили серию коротких эссе по принципам математики, каждое из которых сопровождается красивым, хотя и довольно простым, полноцветным художественным произведением. В каком-то смысле это не столько ужасное сотрудничество, сколько книга вроде 30 Second Maths, где вы получаете мини-экспозицию, сопровождаемую иллюстрацией (хотя я должен сказать, что 30-секундные иллюстрации менее геометрически и, следовательно, обычно более интересны).

Преимущество этой книги по сравнению с 30-секундным подходом состоит в том, что она позволяет Эли Маору предоставить нам значительно больше текста по его темам, так что может быть лучшее исследование и меньше жестких ограничений формата. Для некоторых тем это замечательно, поскольку они действительно нуждаются в дополнительном исследовании. Фигуры Лиссаожу, например, и бесконечные прокладки, подобные треугольнику Серпинского. Но, честно говоря, если вы не математик, трудно слишком увлечься большинством тем.

Возьмите начало сочинения о четырехугольниках.«Вот малоизвестная жемчужина теоремы, — говорит Маор, — которая меня никогда не перестает удивлять: возьмите любой четырехугольник (четырехсторонний многоугольник), соедините середины смежных сторон и — удивительно — вы получите параллелограмм!» Теперь, честно говоря, моя реакция на это была: «Ему следует больше выходить». Точно так же, как только родители могли быть уверены, что их ребенок — самая удивительная вещь, которая когда-либо существовала, только математик нашел бы эту «жемчужину» удивительной.

Итак, если вы получаете удовольствие от всего, от теоремы Пифагора (которая настолько захватывающая, что содержит две записи) до пористости Штейнера (нет, это не заразно), эта книга может быть для вас.Но если вы этого не сделаете, сочинения могут быть местами утомительными, а искусства, хотя и качественно выполненного, никогда не было достаточно, чтобы смотреть на книгу само по себе. Это случай «Хорошая попытка, но у меня это не работает». Это может быть для вас. Что я знаю об искусстве? Но вы пытаетесь это сделать на свой страх и риск. (Между прочим, покупайте книгу Kindle только при просмотре ее на планшете — традиционный черно-белый Kindle потерял бы большую часть художественного воздействия.)

Обзор, впервые опубликованный на сайте www.popularscience.co.uk и размещены здесь с разрешения.

.